Title:
Generalized Theorems of Classical Denoising Methods on Graphs with an
Application to Cancer Classification for Gene Expression Data
Abstract:
Generalized theorems for two Euclidean denoising methods for functions on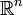 
,
local averaging and kernel regression are proved on graphs. A particular property of Euclidean
denoising which carries over to graphs is that the error of the denoised function decreases to a
minimum as a function of the denoising parameter and then increases. These two numerical
approaches are illustrated for gene expression feature vectors derived from cancer microarrays,
where indices are gene sets with natural graph structures imposed from protein-protein
interactions.