Title:
Avoiding the curse of dimensionality in high dimensional problems
Abstract:
Capturing a function  of a large number (perhaps infinite)
of a large number (perhaps infinite) 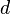 of variables arises
in many application domains. The curse of dimensionality says that the usual
model assumptions based on smoothness and the traditional numerical methods
will suffer the curse of dimensionality. This means using
of variables arises
in many application domains. The curse of dimensionality says that the usual
model assumptions based on smoothness and the traditional numerical methods
will suffer the curse of dimensionality. This means using  samples of the function
or
samples of the function
or  computations will result in an approximation rate which deteriorates severely
with increasing
computations will result in an approximation rate which deteriorates severely
with increasing 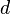 . New ideas to avoid this curse are based on sparsity, compressibility,
and variable reduction. We will discuss how these new ideas avoid the curse and how
numerical methods based on these new ideas should be constructed. For example,
we discuss where one should sample
. New ideas to avoid this curse are based on sparsity, compressibility,
and variable reduction. We will discuss how these new ideas avoid the curse and how
numerical methods based on these new ideas should be constructed. For example,
we discuss where one should sample  in these scenarios.
in these scenarios.
 of a large number (perhaps infinite)
of a large number (perhaps infinite) 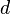 of variables arises
in many application domains. The curse of dimensionality says that the usual
model assumptions based on smoothness and the traditional numerical methods
will suffer the curse of dimensionality. This means using
of variables arises
in many application domains. The curse of dimensionality says that the usual
model assumptions based on smoothness and the traditional numerical methods
will suffer the curse of dimensionality. This means using  samples of the function
or
samples of the function
or  computations will result in an approximation rate which deteriorates severely
with increasing
computations will result in an approximation rate which deteriorates severely
with increasing 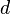 . New ideas to avoid this curse are based on sparsity, compressibility,
and variable reduction. We will discuss how these new ideas avoid the curse and how
numerical methods based on these new ideas should be constructed. For example,
we discuss where one should sample
. New ideas to avoid this curse are based on sparsity, compressibility,
and variable reduction. We will discuss how these new ideas avoid the curse and how
numerical methods based on these new ideas should be constructed. For example,
we discuss where one should sample  in these scenarios.
in these scenarios.